ORIGIN

LeetCode 218. The Skyline Problem

2023-01-31

Problem Description

A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.

The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:

lefti is the x coordinate of the left edge of the ith building.
righti is the x coordinate of the right edge of the ith building.
heighti is the height of the ith building.

You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of “key points” sorted by their x-coordinate in the form [[x1,y1],[x2,y2],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline’s termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline’s contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]

Example 1:

Analysis

Pre-analysis

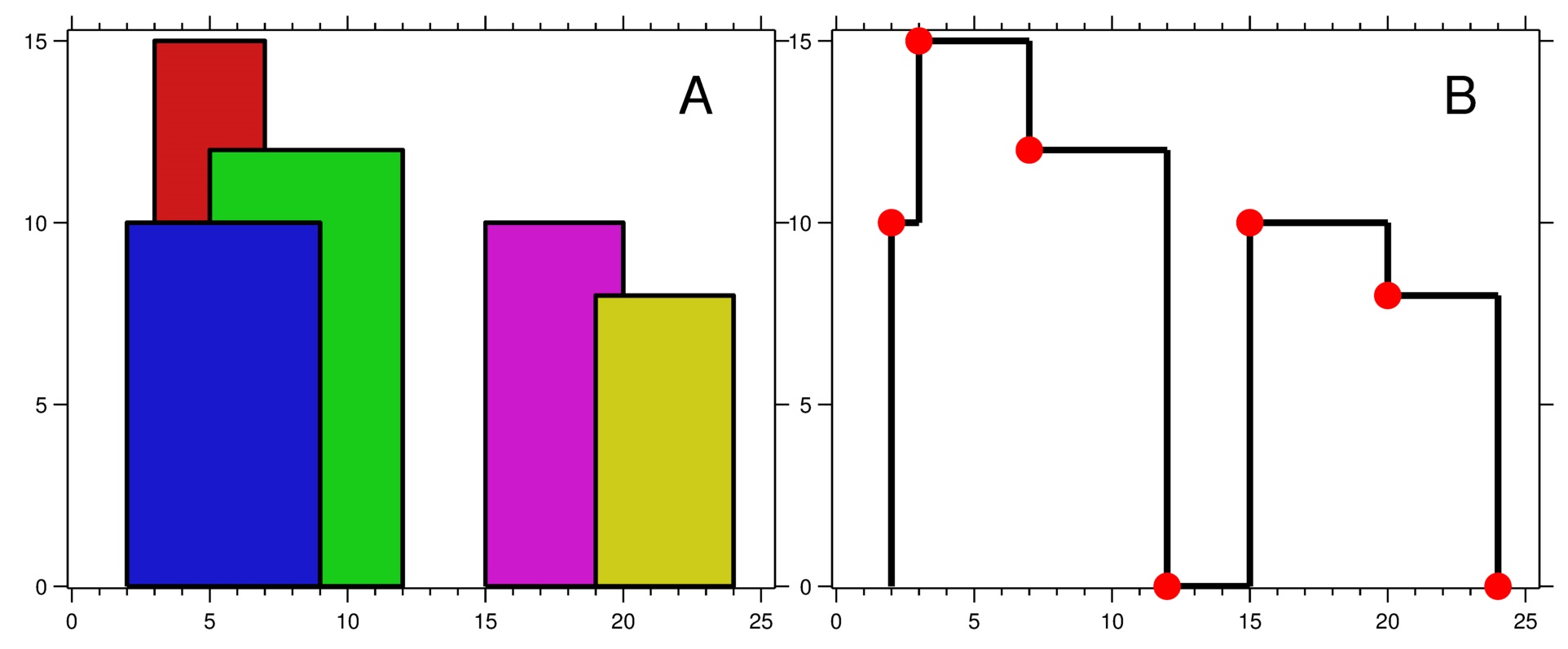
Let’s draw the sky line first with out the graph but with the bunch of input numbers.

We start from the leftmost building. $[2, 9, 10]$. We draw the left line of the building because the left line is not obscured by any other building.

Then we record the right line of the building, because we don’t know whether it will be covered or not.

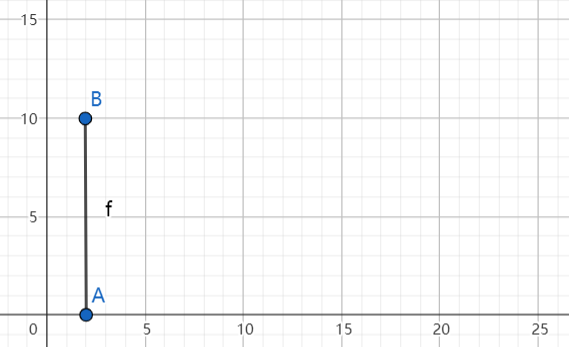
So the recorded lines are now $[line(9, 10)]$

Noticed that after $point B$, we started to draw horizontal line to right, so we know that the height is greater than the original height 0. So we record the point B. $[B] $

Also we save the height of this building [10]
Draw the second building as the same. $[3, 7, 15]$

The second building stars from 3, so we move B horizontally to C

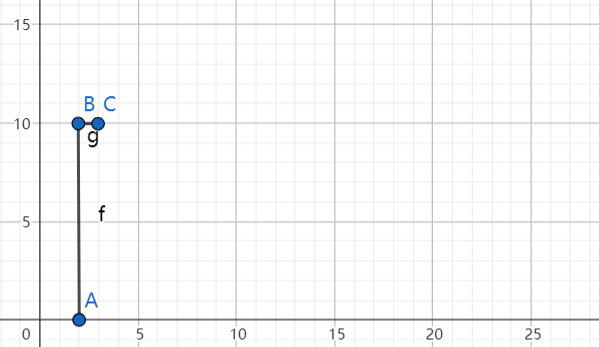
Then starts to draw the remaining left line and also puts its right line into the record lines $[line(9, 10), line(7, 15)]$

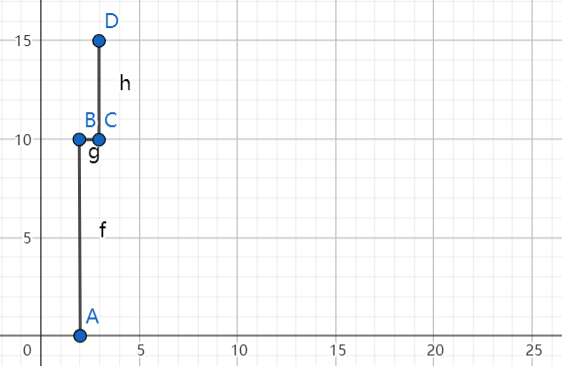
Since the height changes at D, we record the D point to points list: [B, D]

Save height for this building [10, 15]
Let’s look at the third building [5, 12, 12]

We know the current highest building is 15 height, but the height of the third building is only 12 height, so the building is partially covered by the tallest building.

But we also record its right line to lines $[line(9, 10), line(7, 15), line(12, 12)]$

Save height: [10, 15, 12]
Before considering for the next building, we know that the current building’s left lines contains lines that is in front of the next building. So we pick the most front line, line(7, 15).

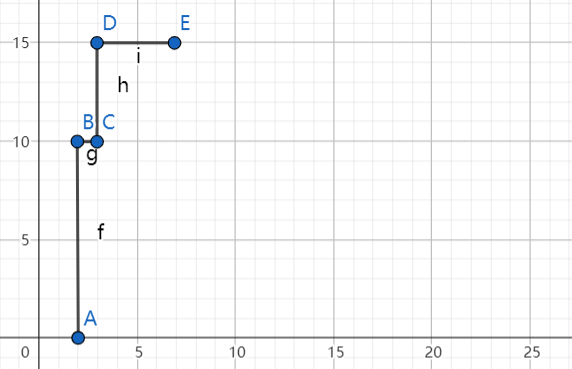
Since E is the right top point of the building, that means we’ve finished drawing the horizontal line of the tallest building, we remove the height from the height list [10, 12].

Now the highest building is at height 12, that means we can only draw down from 15 to 12.

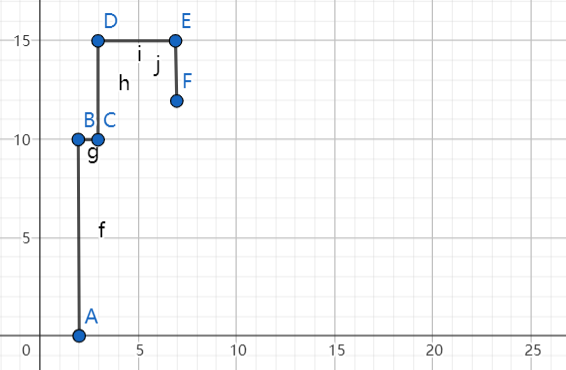
Notice there is a height change at point F, so record F. [B, D, F]
The next right line is line(9, 10). However, the tallest building is now 12 height, so the line(9, 10) is covered within the current tallest building.

Since the right line of the building is finished, we remove the height 10 . heights: [12]
As before, we draw next right line, remove height, and record the next point H

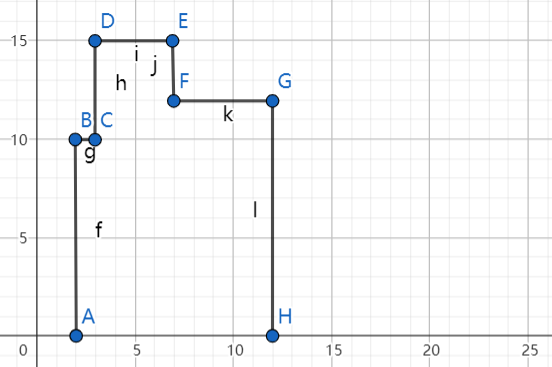
heights: [], right lines: [], record points: [B, D, F, H]
And then, as before, we draw the other two buildings.

Conclude

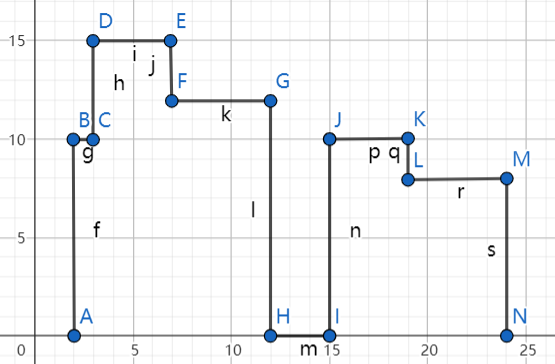
From the analysis above, we distilled the main idea is we need to consider lines as separate parts not dealing the building as a whole.

So instead of adding line to lines list when we meets a new building, we can add the lines together and sort the lines by its position in the x-axis.

In order to distinguish the right line and the left line(because we need to know when to remove height from height list when finish drawing one building), we also need to store that property with other line information.

Also we need to pick the highest buildings each time, so we can store heights in a container that can get the biggest number quickly like Priority Queue or Set to reduce time.

So here comes the question, how do we sort the lines.

The first criteria is that we sort by the x-axis value.
But what if the x-axis value is the same? then we need to distinguish the right and left line.

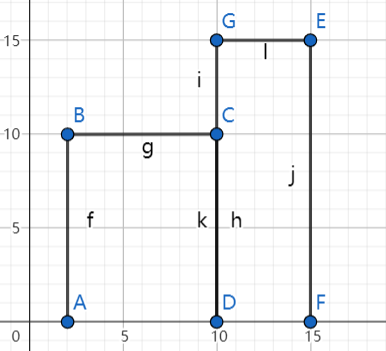
For line $CD$ and $GD$, they have the same x-axis value but are different sides. In this case, we want the left side $GD$ calculate first.

Because if we remove $CD$ first, we max height would become zero(originally 15), which means there is a change in height, so we record point D. that is no the correct point.

So If the x-axis value are the same, we want the left side line gets first
Let’s look at this situation

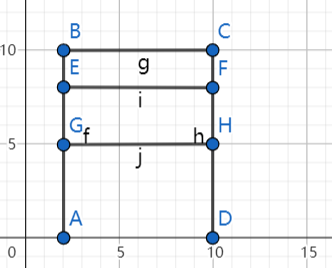
AE, AG are all covered by AB, so we want to calculate the tallest building first. FD, HD are covered under CD, so for the right line, we want to calculate the shorter building because we don’t want to remove the highest height so quickly so that the tallest building changed which actually not.

So, if the x-axis value are the same and they are both left sides, sort by heights in descending order, if both right sides, sort by heights in ascending order.

Sorting criteria summary

bool operator < (const Line& a) const {
    if(xAxis == a.xAxis) {
        if(isRight == a.isRight && isRight == false) {
            return height > a.height; 
        } else if(isRight == a.isRight && isRight == true){
            return height < a.height;
        }
        return isRight < a.isRight;
    }
    return xAxis < a.xAxis;
}

Easy way to sort

There is a tricky thing to write sort easier. Since the left sides and right sides have different order requirements, we can assign the left sides height into negative and sort it in all ascending order.

So we can just sort the lines in x-axis and heights. because left sides’ height are negative, they will appear fronter than the right sides when x-axis are the same.

I use pair<int,int> and sort() will sorts the pairs in ascending order by the first element and then by second element.

Code

class Solution {
public:
    vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
        vector<pair<int,int>> lines;
        vector<vector<int>> ans;
        for(auto i : buildings) {
            lines.push_back(make_pair(i[1], i[2]));
            lines.push_back(make_pair(i[0], -i[2]));
        }
        multiset<int> maxHeight; // there may be many buildings share the same height
        int prevHeight = 0;
        maxHeight.insert(0);
        sort(lines.begin(), lines.end());
        for(auto i : lines) {
            if(i.second > 0) {
                maxHeight.erase(maxHeight.find(i.second)); // jus erase(i.second) will erase all the elements equal to i.second
            } else {
                maxHeight.insert(-i.second);
            }
            int currentHeight = *maxHeight.rbegin(); // .end() is the length of sets
            if(currentHeight != prevHeight) { // there is a height change
                ans.push_back(vector<int>{i.first, currentHeight}); 
                prevHeight = currentHeight;
            }
        }
        return ans;
    }
};