ORIGIN

LeetCode-Container With Most Water

2020-09-06

ACM Logic Two Pointers LeetCode 2 mins424 words

Problem Description

Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

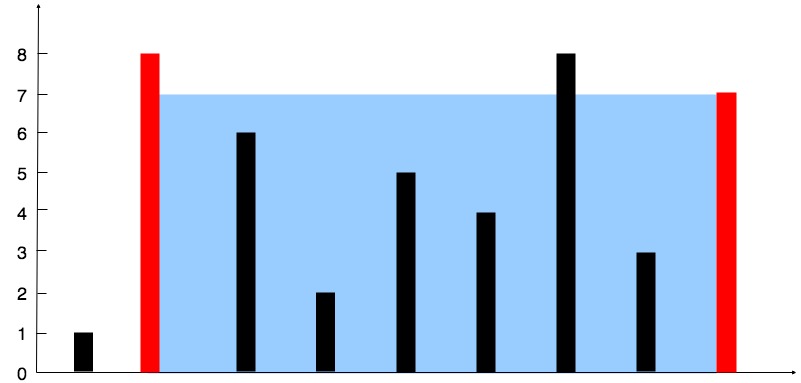
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example:

1 2	Input: [1,8,6,2,5,4,8,3,7] Output: 49

Analysis

Due to the barrel principle, the amount of water that can be in the barrel depends on the shortest plank. So the amount of water between the lines depends on the shortest line.

If you using violence to find all the possibilities and then compare them to find the biggest answer, the time complexity would be very high. So we can use a double pointer, start from the first one and the last one and gradually reduce the distance between the two pointers.

First assume that we start from the front pointer, the pointer stay fixed. So we must move the back pointer.

图片来自公众号《算法爱好者》

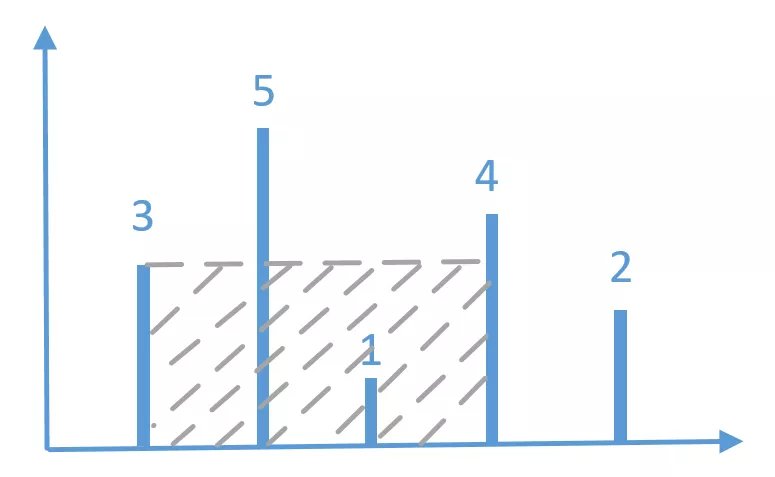
In this graph, the left pointer is line 3. In order to make the area most big, the width also need to be long. So the right pointer starts from line 2 gradually move to line 3.

Each time we move the right pointer one space to the left, the width only minus 1 but the height can change greatly. No matter how the short the height changes, the change in area mainly depends on the change in length.

What we need to do is to find a line that is longer than the 3. We first look 2, then we found 4. So the search comes to an end.

This is just one way search. If we combine the left search with the right search, we need to make the lines with shorter height move. No pointer is fixed.

Code

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0, right = height.size() - 1;
        int area = 0;
        while(left < right) {
            area = max(area, min(height[left], height[right]) * (right - left));
            height[left] < height[right] ? left ++ : right --;
        }
        return area;
    }
};