经验误差与过拟合

**错误率(error rate)**：m个样本中有a个样本分类错误，则错误率 $E=\frac{a}{m}$

**精度(accuracy)**：$1-\frac{a}{m}$

**误差(error)**：实际预测输出与样本的真实输出之间的差异

**训练误差(training error) 经验误差(empirical error)**：在训练集上的误差

**泛化误差(generalization error)**：在新样本上的误差

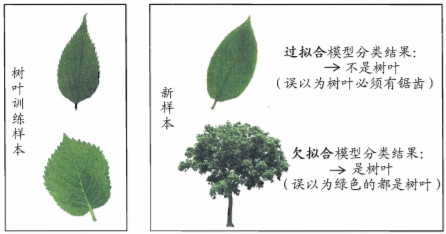
**过拟合(overfitting)**：把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质，导致泛化能力下降

**欠拟合(underfitting)**：对训练样本的一般性质尚未学好

过拟合 、欠拟合的直观类比

评估方法

可通过实验测试来对学习器的泛化误差进行评估并进而做出选择，需要测试集 (testing set)来测试学习器对新样本的判别能力。然后以测试集上的”测试误差” (testing error) 作为泛化误差的近似。通常，我们假设测试样本也是从样本真实分布中独立同分布采样而得，但需注意 是，测试集应该尽可能与训练互斥， 即测试样本尽量不在训练集中出现、未在练过程中使用过.

留出法

“留出法” (hold-out) 直接将数据集D划分为两个互斥的集合，其中一个集合作为训练集S，另一个作为测试集 T，即$D=S∪T,S∩T=ϕ$. 在S上训 练出模型后，用T来评估其测试误差，作为对泛化误差的估计.

交叉验证法

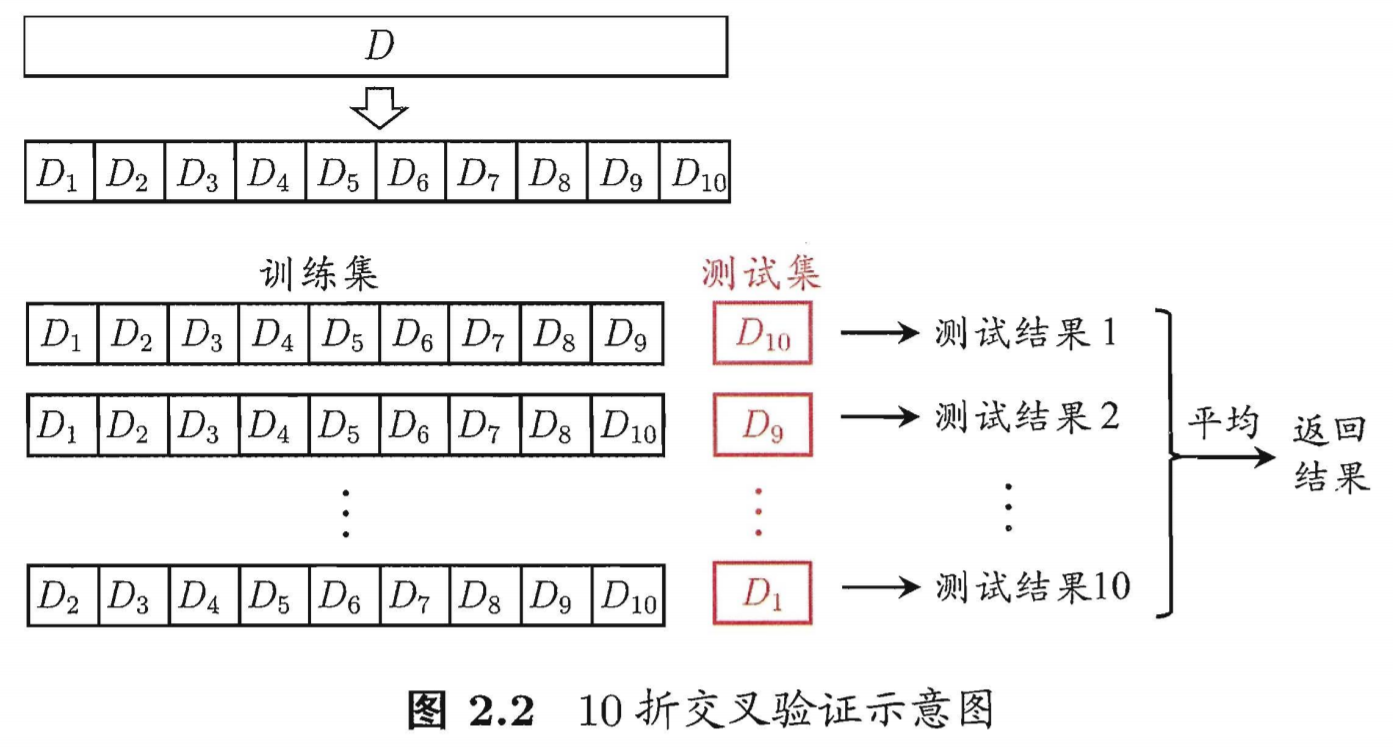
“交叉验证法” (cross alidation)先将数据集D分为k个大小相似的互斥子集，即$D=D1∪D2∪…Dk,Di∩Dj=ϕ(i≠j)$每个子集 $D_1$ 尽可能保持数据分布的一致性，即从D通过分层采样得到. 然后，每次用 k-1 子集的并集作为训练集，余下的那个子集作为测试集;这样就可获得k组训练/测试集，从而可进行k次训练和测试， 最终返回的是 这k个测试结果的均值。显然，交叉验证法评估结果的稳定行和保真性在很大程 上取决于k的取值，为强调这一点，通常把交叉验证法称为“k折交叉验证” (k-fold cross validation). k最常用 的取值是10 ，此时称为10折交叉验；其他常用 的k值有5， 20等.图 2.2 给出了 10 折交叉验证的示意图.

Author: o_oyao

Link: http://dyingdown.github.io/2020/09/09/%E6%A8%A1%E5%9E%8B%E8%AF%84%E4%BC%B0%E4%B8%8E%E9%80%89%E6%8B%A9/

License: All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.