ORIGIN

LeetCode 42. Trapping Rain Water

2023-06-21

ACM DP Array Two Pointers 2P 3 mins495 words

Problem Description

Analysis

We can calculate the water amount by columns.

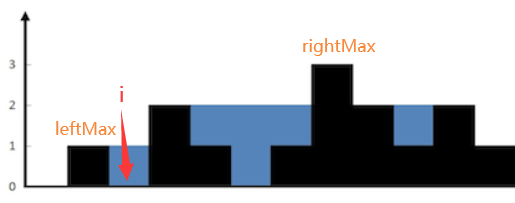
For position i, the water it can contains is based on the left max height column and the right max height columns. And because the capacity of a barrel is determined by the shortest plank it has. So,

The water amount for position i = min(left max height, right max height) - height[i]

Basically, our goal is to find the maximum value on the left and right side for each index.

Method 1: DP

Traverse the the array twice and store the left and right maxs in two same length arrays.

int water = 0, n = height.size();
vector<int> leftMaxArr(n), rightMaxArr(n);
for(int i = 1; i < n - 1; i ++) {
    leftMaxArr[i] = max(height[i - 1], leftMaxArr[i - 1]);
}
for(int i = n - 2; i >= 1; i --) {
    rightMaxArr[i] = max(height[i + 1], rightMaxArr[i + 1]);
}
for(int i = 1; i < height.size()-1; i ++) {
    if(height[i] < leftMaxArr[i] and height[i] < rightMaxArr[i]) {
        water += min(leftMaxArr[i], rightMaxArr[i]) - height[i];
    }
}

Method 2: Two Pointers

Noticed that each maxs in the vector only used once, so we can try to remove the extra space to use only two variable to store it.

It’s easy for the left maxs. we can just let the int variable leftMax change when traversing the heights.

int leftMax = 0;
for(int i = 1; i < height.size()-1; i ++) {
    leftMax = max(leftMax, height[i-1]);
    if(height[i] < leftMaxArr[i] and height[i] < rightMaxArr[i]) {
        water += min(leftMax, rightMaxArr[i]) - height[i];
    }
}

But we cannot do the same for the maximum value on the right side because finding the maximum value on the right requires searching from the first element on the right to the far right in order to determine it. So, we need to use two pointers and start traversing from both the left and right sides simultaneously.

After each update of the left and right pointers, we also calculate the current maximum values on the left and right sides. And we count the first initiate as one update, so in the loop, we start from calculating the current maximum left and right values.

For each update, we need to decide the min of leftMax and rightMax in order to calculate the acount of water for index i(maybe left, or right) .

class Solution {
public:
    int trap(vector<int>& height) {
        int water = 0;
        int leftMax = 0, rightMax = 0,
            left = 0, right = height.size()-1;
        while(left < right) {
            leftMax = max(leftMax, height[left]);
            rightMax = max(rightMax, height[right]);
            if(leftMax < rightMax) {
                if(height[left] < leftMax) {
                    water += leftMax - height[left];
                }
                left ++;
            } else {
                if(height[right] < rightMax) {
                    water += rightMax - height[right];
                }
                right --;
            }
        }
        return water;
    }
};