ORIGIN

Inclusion Exclusion Principle

2019-08-15

Algorithm Knowledge points Math Inclusion Exclusion Principle 3 mins517 words

In combinatorics (combinatorial mathematics), the inclusion–exclusion principle is a counting technique which generalizes the familiar method of obtaining the number of elements in the union of two finite sets; – From Wikipedia

Inclusion-Exclusion Principle

Example: Set A and B

$|A∪B|=|A|+|B|−|A∩B|$

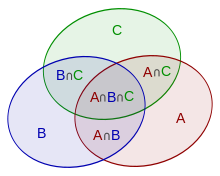
Set A, B and C

$|A∪B∪C|=|A|+|B|+|C|−|A∩B|−|A∩C|−|B∩C|+|A∩B∩C|$

So we get a normal function:

Example

Co-prime

Given a number N, you are asked to count the number of integers between A and B inclusive which are relatively prime to N.

Two integers are said to be co-prime or relatively prime if they have no common positive divisors other than 1 or, equivalently, if their greatest common divisor is 1. The number 1 is relatively prime to every integer.

Input

The first line on input contains T (0 < T <= 100) the number of test cases, each of the next T lines contains three integers A, B, N where (1 <= A <= B <= 10 15) and (1 <=N <= 10 9).

Output

For each test case, print the number of integers between A and B inclusive which are relatively prime to N. Follow the output format below.

Sample Input

1
2
3

2
1 10 2
3 15 5

Sample Output

1 2	Case #1: 5 Case #2: 10

Code

This is just an easy application of the Inclusion-Exclusion Principle. Find the numbers that are not co-prime and cut it of from the given number range.

#include<bits/stdc++.h>

using namespace std;

long long arr[100000]; // used to store the prime fators of n

long long prime_factor(long long n){ // Calculate the prime factors of n
	long long count = 0;
	for(long long i = 2; i * i <= n; i ++){
		if(n % i == 0){
			count ++;
			arr[count] = i;
		}
		while(n % i == 0){
			n /= i;
		}
	}
	if(n != 1){
		count ++;
		arr[count] = n;
	}
	return count; // the kinds of prime factors 
}
int main(){
	long long t, a, b, n;
	cin >> t;
	for(long long s = 0; s < t; s ++){
		cin >> a >> b >> n;
		memset(arr, 0, sizeof(arr));
		long long count = prime_factor(n);
		long long sum = 0; 
        // i in binary stands for all situation if the nth is selected
		for(long long i = 1; i < (1 << count); i ++){ // i << count = 2^count
			long long sumi = 1, counti = 0; 
            // sumi is ultimate number correspond to this situation
			for(long long j = 0; j < count; j ++){
				if(1 & (i >> j)){ // i shifts j to the right and if odd number
					sumi *= arr[j + 1];
					counti ++;
				}
			}
			if(counti & 1){ // is the selected set number is odd number
				sum += b / sumi;
				sum -= (a - 1) / sumi;
			}else{
				sum -= b / sumi;
				sum += (a - 1) / sumi;
			}
		}
		printf("Case #%lld: %lld\n", s + 1, b - a + 1 - sum);
	}
	return 0;
}